Difference between revisions of "Sudoku"
(→Usage: adjusted textual appearance of scratchpad sample) |
(→Example for using the ScratchPad functionality: added screenshot) |
||
| Line 49: | Line 49: | ||
Pressing the Enter key will write back the changes to the ScratchPad, pressing Escape will discard the pop-up form.<br> | Pressing the Enter key will write back the changes to the ScratchPad, pressing Escape will discard the pop-up form.<br> | ||
<br> | <br> | ||
| − | In the example, if now uncheck "6" (leave the "2") and click Ok, then click the "Copy back..." button.<br> | + | [[File:sudoku-scratchpad-digitset-editor.jpg]]<br> |
| + | |||
| + | In the example, if now uncheck "6" (leave the "2") and click Ok, then click the "Copy only values back..." button.<br> | ||
The changes are propagated back to the main form.<br> | The changes are propagated back to the main form.<br> | ||
Again click the "Solve" button.<br> | Again click the "Solve" button.<br> | ||
Latest revision as of 22:54, 10 January 2020
│
Deutsch (de) │
English (en) │
español (es) │
français (fr) │
About
There is very little to tell about this program. It is just an attempt to make a program which solves Sudoku puzzles.
License
See the sources. I just hope it is a useful demo. Useful as in you can learn something from it.
Author
Matthijs Willemstein
Modifications by Bart
Download
The sources can be found at the Lazarus-CCR repository and can be obtained via svn:
svn co https://svn.code.sf.net/p/lazarus-ccr/svn/applications/sudoku/ local/path/to/sudoku
Alternatively you can view the sources through viewcv:
https://sourceforge.net/p/lazarus-ccr/svn/HEAD/tree/applications/sudoku/
Usage
If you run the program you will see a grid, and two buttons. If you press the "Edit" button, you are able to edit the grid and place the numbers in the grid according to your puzzle.
If you press the "Clean" button, the grid will be cleared.
When you are finished entering the digits press "Solve" and the grid will be filled with the solution.
If the program is unable to completely solve the Sudoku, a ScracthPad form will pop up.
This form shows for each cell what possible options are left.
Solved cells will contain a single number, unsolved will have a range of possibilities, shown as commaseparated values enclosed in brackets, arranged in rows of three:
|1 | | 4 | |7 9|
In the above example, the numbers 1, 4, 7, and 9 are in the range of possibilities.
You can edit the grid and copy the values back to the main form, then try to solve it again.
(Note: only cells that contain a single digit will be copied back to the main form.)
The program also has the option to load and save sudoku files.
A sample sudoku file is incuded in the svn repository.
The file format is a simple textfile, it is explained in the sources.
Example for using the ScratchPad functionality
The sample file "unsolvable.sudoku" (included in the repository) cannot be solved by the program.
If you load it and then click Solve, the ScratchPad will pop up.
Now click on the second cell in the bottom row.
An editor will pop up.
The editor has 9 checkboxes. In this example the checkboxes for "2" and "6" should be checked.
You can toggle a checkbox's state by either (as usual) clicking ont it, or pressing the number ("1".."9") on the keyboard.
Pressing the Enter key will write back the changes to the ScratchPad, pressing Escape will discard the pop-up form.
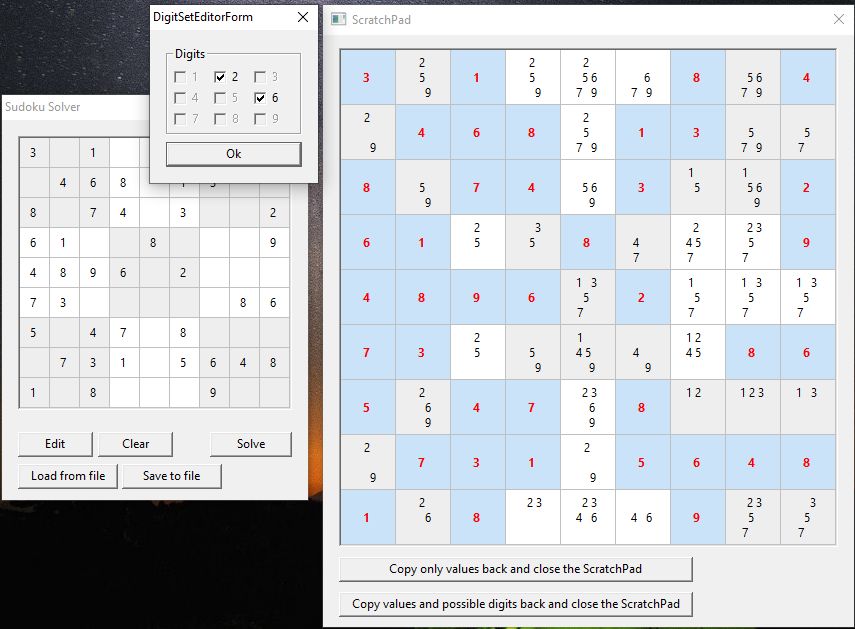
In the example, if now uncheck "6" (leave the "2") and click Ok, then click the "Copy only values back..." button.
The changes are propagated back to the main form.
Again click the "Solve" button.
The program now will be able to solve the Sudoku.
Description
The programs solves all Sudoku puzzles that can be solved by logic. It will not solve the puzzle where you need to guess for a solution.
So it follows these rules (taken from WebSudoku):
The rules of Sudoku are simple. Enter digits from 1 to 9 into the blank spaces. Every row must contain one of each digit. So must every column, as must every 3x3 square. Each Sudoku has a unique solution that can be reached logically without guessing.
Related Sites
Sudoku Solver Online Sudoku Solver Released Under The GNU public license.